Surface Waves
Relating to work conducted from 2006 to 2008
 As was shown in the section on nano acoustics when a laser pulse is incident on a metal structure it leads to rapid heating and cooling, and subsequently an acoustic pulse is generated. When this is done on a film of metal a strain pulse will be generated which spreads over the surface in much the same way as the ripples on a pond. Each pulse will generate one surface wave, as they are known, and these will travel across the metal surface until they are absorbed by the material. The height of these waves above the surface, is small, in fact it is less than the width of an atom, so some very sensitive techniques are required to view the waves. To do this an interferometer is used. Here instead of one probe pulse we now have two, separated in time by less than a nano second. These two pulses hit the same point on the surface and are then recombined to form a single pulse again. If no surface wave is present the two pulses combine perfectly and there is no signal. However, if a surface wave is present the surface will be at different height for the two pulses, so they will travel slightly different distances, and when they recombine this difference will amount to a small signal. Again, by using optical and electrical techniques this signal can be observed and then the techniques are applied to image the surface at different points in space and time to create a reconstruction of the wave motion.
As was shown in the section on nano acoustics when a laser pulse is incident on a metal structure it leads to rapid heating and cooling, and subsequently an acoustic pulse is generated. When this is done on a film of metal a strain pulse will be generated which spreads over the surface in much the same way as the ripples on a pond. Each pulse will generate one surface wave, as they are known, and these will travel across the metal surface until they are absorbed by the material. The height of these waves above the surface, is small, in fact it is less than the width of an atom, so some very sensitive techniques are required to view the waves. To do this an interferometer is used. Here instead of one probe pulse we now have two, separated in time by less than a nano second. These two pulses hit the same point on the surface and are then recombined to form a single pulse again. If no surface wave is present the two pulses combine perfectly and there is no signal. However, if a surface wave is present the surface will be at different height for the two pulses, so they will travel slightly different distances, and when they recombine this difference will amount to a small signal. Again, by using optical and electrical techniques this signal can be observed and then the techniques are applied to image the surface at different points in space and time to create a reconstruction of the wave motion.
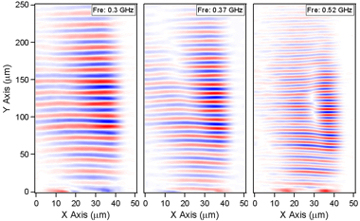 The ability to watch these surface waves has a number of applications. As a first example, a surface wave is produced on the edge of a thin copper plate. Instead of exciting a point, as schematically shown above, a bar shape is excited so as to produce a set of plane waves. These travel along the edge of the copper plate and are imaged as discussed above. Next, the Fourier transform of the set of images in time is taken to show the amplitude of the oscillations on the surface for each frequency. This is a hard to visualise but when considering the figure shown here it can be seen that for each of the three images the spacing between the red and blue lines get smaller in successive shots (shorter wavelength means higher frequency). In the real case the wave that passed over the surface contained all these frequencies; the images show how each frequency component saw the surface individually. The interesting feature of the three images is the white line diagonally intersecting the red-blue waves. If looked at closely, the wavelength of the red-blue waves travelling up the image is slightly different either side of the thick white diagonal line, and as the frequency is increased this difference becomes more pronounced and the white separating line become clearer and more vertical.
The ability to watch these surface waves has a number of applications. As a first example, a surface wave is produced on the edge of a thin copper plate. Instead of exciting a point, as schematically shown above, a bar shape is excited so as to produce a set of plane waves. These travel along the edge of the copper plate and are imaged as discussed above. Next, the Fourier transform of the set of images in time is taken to show the amplitude of the oscillations on the surface for each frequency. This is a hard to visualise but when considering the figure shown here it can be seen that for each of the three images the spacing between the red and blue lines get smaller in successive shots (shorter wavelength means higher frequency). In the real case the wave that passed over the surface contained all these frequencies; the images show how each frequency component saw the surface individually. The interesting feature of the three images is the white line diagonally intersecting the red-blue waves. If looked at closely, the wavelength of the red-blue waves travelling up the image is slightly different either side of the thick white diagonal line, and as the frequency is increased this difference becomes more pronounced and the white separating line become clearer and more vertical.
 The origin of this feature is a thinning of the copper plate near the edge. As the copper becomes thinner the waves travel at different speeds, leading to the different observed wavelengths. This effect results in a waveguide effect near the edge. Using this technique, it is hence possible to analyse the exact geometries of metal surfaces in exquisite detail, which can be valuable when considering micro and nano engineering.
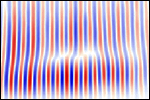
As a further interesting use of this technology, it is possible to watch the way surface waves interact with more complex structures. The figure, right, shows a simulation of surface waves incident on a set of micron sized triangles. The wave arrives as a pulse travelling from left to right. As the wave hits the triangles much of its energy is reflected. If, however, the experiment is repeated with the wave travelling from right to left the wave propagates through the structure more effectively. The image shows the results of simulations but work on real structures has also been conducted and the results show that the devices do work as acoustic rectifiers. Whilst appearing to be quite niche surface waves are routinely used in mobile phones when converting acoustic signals, and so greater understanding and control over these waves can have great potential future value.
The origin of this feature is a thinning of the copper plate near the edge. As the copper becomes thinner the waves travel at different speeds, leading to the different observed wavelengths. This effect results in a waveguide effect near the edge. Using this technique, it is hence possible to analyse the exact geometries of metal surfaces in exquisite detail, which can be valuable when considering micro and nano engineering.
As a further interesting use of this technology, it is possible to watch the way surface waves interact with more complex structures. The figure, right, shows a simulation of surface waves incident on a set of micron sized triangles. The wave arrives as a pulse travelling from left to right. As the wave hits the triangles much of its energy is reflected. If, however, the experiment is repeated with the wave travelling from right to left the wave propagates through the structure more effectively. The image shows the results of simulations but work on real structures has also been conducted and the results show that the devices do work as acoustic rectifiers. Whilst appearing to be quite niche surface waves are routinely used in mobile phones when converting acoustic signals, and so greater understanding and control over these waves can have great potential future value.
Papers relating to this work:
 Optical generation of surface acoustic waves guided at the linear boundary between two thin films
Optical generation of surface acoustic waves guided at the linear boundary between two thin films
A.A. Maznev, T.A. Kelf, M. Tomoda, O. Matsuda, and O.B. Wright
J. Appl. Phys.107, 033521 (2010)
 Real-time imaging of acoustic rectification
Real-time imaging of acoustic rectification
S. Danworaphong, T.A. Kelf, O. Matsuda, M. Tomoda, Y. Tanaka, N. Nishiguchi, O.B. Wright, Y. Nishijima, K. Ueno, S. Juodkazis, and H. Misawa.
Appl. Phys. Lett. 99, 201910 (2011)