Surface Plasmon Polaritons
Relating to work conducted from 2002 to 2006
A nice example of surface plasmon polaritons (or surface plasmons for short) is in the Lycurgus Cup (picture). This was made in Roman times and under normal lighting appears green. However, when illuminated from within it becomes red in colour. This is a similar effect to the butterfly's wing , in that the colours are being filtered. However, it is found that the size of the structures involved in this filtering process are around 100 times smaller than the wavelength of light, so something different must be happening compared to the case of the wing. For the wing it was only the size of the structuring that was important, in the cup, as in all stain glass windows, it is the material that is important. It is tiny metal particles that produce the colours. From everyday experience it is clear that metals interact strongly with light - a mirror being the best example, the light is forced to turn around and travel in the opposite direction whenever it meets a mirrored surface. The reason for this is that metals have free electrons floating around in them. Light and electrons have an intimate connection due to their electric fields, for a mirror the oscillation of the light field causes the electrons in the metal to also oscillate. Because the electron has some mass it takes time to get them moving and so, in the simple case considered here, they tend to oscillate in anti-phase with the optical field (if the field is moving left the electrons are moving right).
This movement stops the light from entering the material, the electrons create a screening field that the light cannot pass through, and so, since the light has to go somewhere, it is reflected. In the case of the cup the pieces of metal are so small that this picture no longer works. It has to be remembered that all things are quantum in nature at the small scale, and so everything is a wave. The free electrons moving around the particles can only oscillate at certain frequencies corresponding to the allowed standing waves (like waves on a sting) - this is the simplest definition of a surface plasmon, an oscillation of the free electrons at the surface of a metal at a certain frequency. At these frequencies the light is highly absorbed and scattered, leading to a much-reduced transmission but enhanced reflection, giving the cup its properties. By altering the size of the metal particles, the scattered colours (and therefore transmitted colours) can be altered, providing the means to make the colours seen in stained glass.
For larger surfaces things are a little different, but the same general rules apply: structuring can cause standing waves in the free electrons of a metal, and this can create surface plasmons. Since transmission is impossible in this case (there is a block of metal under the surface), the plasmon will appear as an absorption of a certain colours in the reflected light.
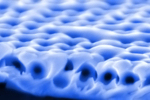
The surfaces studied during my PhD are both made from metal and structured on the optical scale, so one can expect a maximisation of optical interactions. To study these in detail the reflectivity of the surface is recorded as a function of the incident angle, orientation and position on the sample (this corresponds to different dish geometries, as seen before). A white light laser is used to get accurate data and allows us to look at all wavelengths in the visible and infrared regions of the spectrum. This is a lot of parameters, and rather than spending a lifetime in a dark room we built a computer-controlled system to record the thousands of spectra needed for each sample (picture above). Because the surfaces have six-fold symmetry, things are expected to follow this trend, and indeed the diffracted light does possess a six-fold symmetry, as shown in the picture. It should be noted that the intensity of the diffracted light is tiny compared to the reflected beam and so can be ignored in all other analysis.
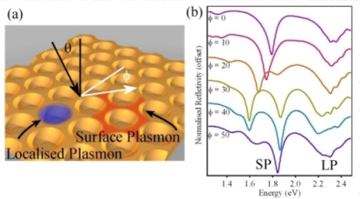Rather than jump straight into the masses of accumulated data it is perhaps worth looking at a few representative reflectivity spectra to understand some of the physics, these are shown opposite. These spectra show the intensity of the reflected beam at different energies (this is equivalent to the frequency of the light), the incident angle is kept constant and each spectra shown is a rotation of the sample by 10 degrees (this is done up to 60 degrees, after this the pattern repeats 6 times due to the symmetry). There are essentially two features, marked SP (surface plasmon) and LP (localised plasmon). Here, I'm afraid, I must alter the definition of words a little. Both the plasmons mentioned are types of surface plasmon, however their behaviour is very different and rather than use a lengthily phrase to describe each I will simple refer to surfaces plasmons that are trapped within voids as 'localised' and those that roam over the surface as 'surface'.
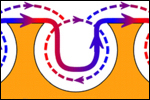
So far only localised plasmons have been discussed, standing waves. These localised plasmons are found to be trapped within the dishes, as shown in the accompanying cartoon. Since they are trapped, they know nothing of the rest of the sample and always absorb the same energy of light regardless of sample orientation or incident angle - hence do not change with the angle in the different spectra. What I now define as a surface plasmon is one that flows over the surface, bouncing between the voids. Because these plasmons are not trapped they are not strictly standing waves; however, they sometimes bounce back and forth between voids, and this sets up a kind of standing wave. These surface plasmons, therefore, feel the symmetry of the surface and absorb varying amounts of light at different energies, depending on the sample orientation, as shown in the absorption spectra.
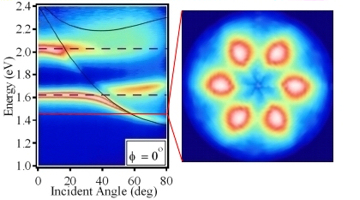The next images are a little more complicated but nothing has changed, simply more parameters have been added. Now the energy of the light is on the y-axis and the incident angle of the laser beam is plotted on the x-axis. The amount of absorption is signified by the colour of each image pixel, running from blue (no absorption) to white (max absorption). Again, two types of feature are present. The energy of two horizontal absorption features can be seen to be independent of incident angle, as indicated with the dashed lines; these are the localised plasmons. A further feature can be seen to change energy with incident angle, the solid lines represent the theoretical behaviour of these surface plasmons and a good fit can be seen. The second image shows the results when a single energy (as indicated with the red line) is observed with incident angle plotted from the centre of the circle to the edge and sample orientation plotted around the circle. As might be expected the surface plasmon absorption has a six-fold symmetry, again due to the surface structure.
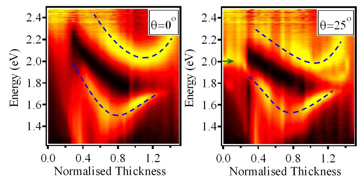A slightly more complex image is shown in the next figure. Now incident angle and sample orientation are kept at zero and the data shows how the energy of the different plasmon features varies with sample geometry (using the definition of normalised thickness where 1 corresponds to a surface thickness equal to the initial template sphere's diameters - i.e. this should look like a flat surface with spherical bubbles under it. A normalised thickness of, 0.1, therefore corresponds to shallow dishes, see the nano-structure section). The colour scale now runs from black (no absorption) to yellow (all of the incident light is absorbed). It is found that surface plasmons are independent of sample geometry and are constant in energy; at normal incidence they are only weakly excited and not clear in the image. The important factor in this image is that the localised plasmons vary in a complicated way with sample geometry. A full understanding of this behaviour is very involved, however, as an approximation it can be understood that as the dishes become more like spherical voids the localised plasmons become more confined, leading to a decrease in energy. For a further discussion please see
plasmon interactions section.
With this understood many interesting experiments can be performed, notable the observations of what happens when localised and surface plasmons are forced to interact, this gets more in-depth so if you're interested see the plasmon interactions section or the presented work section of this website.
While much of the work presented above is purely out of academic interest, there are several possible applications for plasmon engineering, perhaps the most promising being that of Surface Enhanced Raman Scattering, where the plasmonic activity of the surface enhances the interaction of light with trace levels of molecules.
Papers relating to this work:
Localized and delocalized plasmons in metallic nanovoids
T.A. Kelf, Y. Sugawara, R.M. Cole, J.J. Baumberg, M.E. Abdelsalam, S. Cintra, S. Mahajan, A.E. Russell, and P.N. Bartlett.
Phys. Rev. B. 74, 245415 (2006)
Also selected to appear in the Virtual Journal of Nanoscale Science and Technology.
Plasmonic bandgaps and Trapped Photons on Nanostructured Metal Surfaces
T.A. Kelf, Y. Sugawara, J.J. Baumberg, M.E. Abdelsalam, P.N. Bartlett.
Phys. Rev. Lett. 95, 116802 (2005)
Also selected to appear in the Virtual Journal of Nanoscale Science and Technology.
Thesis: Light-Matter Interactions on Nano-Structured Metallic Films
Work carried out at the University of Southampton under the supervison of Prof. J.J. Baumberg